Trucklover
BNSF SD70MAC's
Hi Guys
A while back i built this photo diorama so i could take some pics of my trains and trucks on when i dont have a layout, like right now lol
Anyways, here is how i did it

View looking right down the Diorama. Single Track is raised in the back.

You can see my grandmas dog in the bottom left corner, she likes to help hehe. You can also see how the roads will be layed out, 2 lanes going East and 2 lanes going West, Only one of the lanes going West is blocked off due to construction. There will also be a center divider in between the East and Westbound lanes.

You can see that the road dead ends here. Thats because the Black Gold Asphalt Plant is just to the right. The road goes North and under the train track. Lots of construction will be going on. I just layed stuff out as a general guideline for me and taking the pics so you guys could see how this will be layed out.

Black Gold Asphalt Plant sits at the far right of the Diorama

View from the back of the Asphalt Plant

View from the back of the Highway Underpass

Back of the Construction Site

Here you can get a better sense of how the roads and such will be layed out. 2 Lanes run Eastbound on the bottom of the display, and 2 lanes run Westbound (again one is blocked off due to construction), a Center Divider separates the East and Westbound lanes, and in the top of the picture you see where the Embankment running from where the train track is down to the highway.
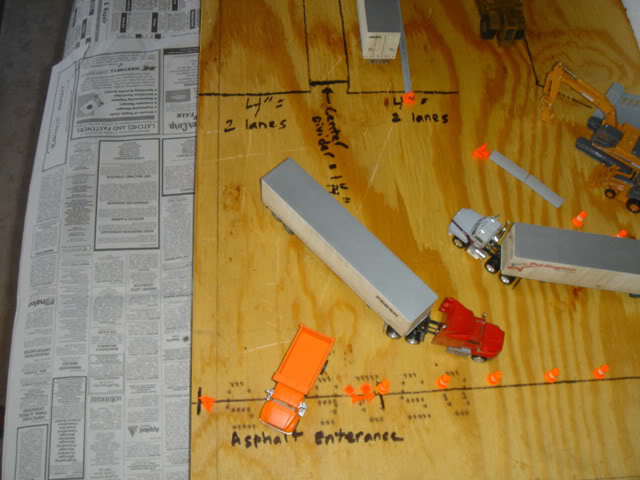
Highway lanes are 4" wide (or 2" per lane), Center Divider is 1 1/4, and the Black Gold Asphalt Entrance is marked at the bottom of the pic.
A while back i built this photo diorama so i could take some pics of my trains and trucks on when i dont have a layout, like right now lol
Anyways, here is how i did it
View looking right down the Diorama. Single Track is raised in the back.
You can see my grandmas dog in the bottom left corner, she likes to help hehe. You can also see how the roads will be layed out, 2 lanes going East and 2 lanes going West, Only one of the lanes going West is blocked off due to construction. There will also be a center divider in between the East and Westbound lanes.
You can see that the road dead ends here. Thats because the Black Gold Asphalt Plant is just to the right. The road goes North and under the train track. Lots of construction will be going on. I just layed stuff out as a general guideline for me and taking the pics so you guys could see how this will be layed out.
Black Gold Asphalt Plant sits at the far right of the Diorama
View from the back of the Asphalt Plant
View from the back of the Highway Underpass
Back of the Construction Site
Here you can get a better sense of how the roads and such will be layed out. 2 Lanes run Eastbound on the bottom of the display, and 2 lanes run Westbound (again one is blocked off due to construction), a Center Divider separates the East and Westbound lanes, and in the top of the picture you see where the Embankment running from where the train track is down to the highway.
Highway lanes are 4" wide (or 2" per lane), Center Divider is 1 1/4, and the Black Gold Asphalt Entrance is marked at the bottom of the pic.
Last edited by a moderator:

